These Market Truths Are Not Self-Evident
Many of those who teach the fundamentals of investing hold a few concepts sacred, like the concept of efficient markets, portfolio management theories, and, most sacred of all, the capital asset pricing model, or CAPM. It is taught in classrooms around the world, tested in exams crowning chartered financial analysts, and used by analysts as the basis for their financial models.
But does it really make sense? The events of recent years should turn this theory on it head, if not lead us to throw it out the window altogether.
What is the capital asset pricing model?
The CAPM is a model that calculates the expected return of an asset based on risk, the expected return of the market over a risk-free asset, and the risk-free rate. The formula looks like this:
Expected rate of return = risk-free rate beta X market risk premium
But these variables have some major flaws that academics and investors often gloss over.
Risk-free rate
The risk-free rate is the rate of return an investor should expect in a riskless asset. What is a riskless asset? We could debate that all day. Perhaps it's gold, silver, or a strong education -- except it's not. The market has decided that Treasuries are risk-free. Why? Because they pay an interest rate and there wasn't a better alternative.
How risk-free are Treasuries or sovereign debt in general? I would argue that they're quite risky.
The idea that sovereign debt is risk-free forgets a history of countries defaulting, or at least changing the rules about the debts they have accumulated. This past weekend on Fareed Zakaria GPS, Philip Coggan argued that for centuries sovereign nations have posed a number of risks for creditors. Countries have inflated currencies by adding copper or lead to coins and printed money to pay off debt, just like we're doing today. And outright defaults aren't out of the ordinary, either.
Look at what's happening in Greece, where the rules are different for private creditors and public creditors. Greece is defaulting to private creditorsNational Bank of Greece (NYS: NBG) and Deutsche Bank, essentially hanging all of the risk on those who thought the country's sovereign debt was relatively riskless. Since when do some creditors have to take the fall while others don't? A world in which the rules can be changed before your eyes seems fraught with risk to me.
Even though I don't believe in investing in gold, I could make an argument that buying gold through something like SPDR Gold Trust ETF (NYS: GLD) would be less risky than buying Treasuries. In 1,000 years, it's likely that gold will still have value, while the likelihood that the U.S. government will not have defaulted is pretty small (if history teaches us anything).
Beta
This is probably the most flawed assumption used in CAPM, because beta isn't a measure of risk at all. Beta is actually a measure of volatility. But since the market hasn't found a good way to boil risk down into a single number, this is the best academics can do. How effective is it?
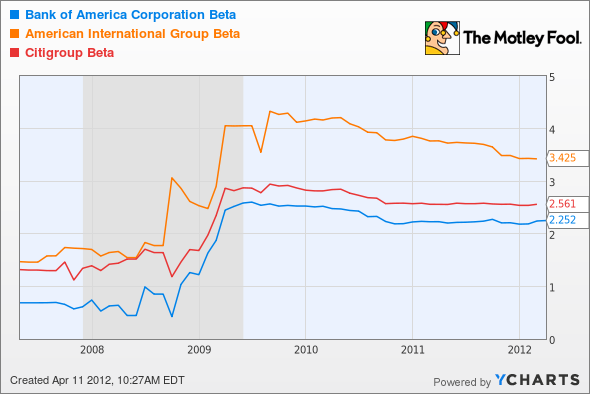
Those who invested in financials before the recession have an idea how effective beta is as a measure of risk. Bank of America (NYS: BAC) had a beta of 0.48 at the beginning of 2007, indicating that it was less risky than the market. Before the recession, AIG (NYS: AIG) and Citigroup (NYS: C) had betas of around 1.5, dramatically underestimating the eventual volatility in their subsequent movements as each hovered on the brink of failure before the government stepped in.
Risk is a tough concept to understand, and maybe a single number isn't able to capture its essence -- specially a number that is more concerned with volatility in the stock market than anything involving the actual business.
Market risk premium
The market risk premium assumes that we know what the market rate of return is and what the risk-free rate is. I argued above that we don't know the latter, and getting a result for the former is a guess at best.
The market rate of return could be the average return over a period of time, the return of stocks regressed on a chart based on beta, or any other number of guesses. But is any figure better than another? And is any one correct? I would say no.
So how can we possibly predict what premium, or overall rate of return, investors expect from the market? Maybe asking them would be a better solution.
Foolish bottom line
I've heard the academics talk about the virtues of CAPM, and I've seen its work in analyst models. What I've come to accept is that no one has a better way to build a theory about the stock market. It has to make sense, doesn't it? There must be a formula!
Or maybe there mustn't. Maybe there are too many variables to boil into a few simple numbers. Maybe risk simply can't be quantified as easily as we hope. Maybe there's an art to investing or some level of analysis that doesn't involve formulas and statistics.
There may not be a magic formula, but our analysts have a solid record of beating the market using easy-to-understand logic and strategic analysis. In the free report here, they'll outline three stocks that are great for the long term.
At the time thisarticle was published
Copyright © 1995 - 2012 The Motley Fool, LLC. All rights reserved. The Motley Fool has a disclosure policy.